Introduction to Calorimetry

Learning Outcomes

  • Apply the safety rules in the chemistry laboratory through proper and safe handling of chemicals and chemical equipment.
  • Identify and use common equipment and measuring devices in the chemistry laboratory.
  • Properly record experimental data including the precision appropriate to the measuring devices used.
  • Properly make measurements of length, mass, volume, and temperature.
  • Properly perform the technique of filtration, quantitative transfer of materials, pipetting and use of the Bunsen burner.
  • Tabulate and graph experimental data.
  • Apply the steps of the scientific method.
  • Determine energy changes in chemical reactions.

 Specific heat capacity () is the amount of heat energy required to raise the temperature of 1 gram of a substance by 1°C (or 1 K). Each substance has its own unique specific heat value, which determines how quickly it heats up or cools down. For example, water has a relatively high specific heat of 4.18 J/g·°C, meaning it requires more energy to change its temperature compared to aluminum (0.89 J/g·°C) or copper (0.39 J/g·°C). In this experiment, you will determine specific heat using a coffee cup calorimeter, which consists of two nested Styrofoam cups with a lid to minimize heat loss. A thermometer or digital temperature probe will be used to measure initial and final temperatures of the water and metal, and a digital balance will measure the mass of both. A hot plate or boiling water bath will heat the metal to a known temperature, and tongs will safely transfer the hot metal to the calorimeter. Together, these tools allow for accurate measurement of heat transfer and calculation of specific heat capacity.

Coffee Cup Calorimeter Diagram

Here is a simple illustration of how your setup might look:

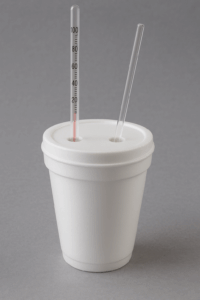
A coffee cup calorimeter.
Image generated by OpenAI’s DALL·E.

In this lab, we will make the simplifying assumption that no heat is lost to the surrounding environment. Under this assumption, the heat released by the hot metal cylinder when it is placed into cooler water is exactly equal to the heat absorbed by the water:

qmetal=−qwater​Since heat () can be calculated using the equation q = m × C × ΔT, we can substitute into the relationship above:

mmetal⋅Cmetal⋅ΔTmetal=−(mwater⋅Cwater⋅ΔTwater) 

Rearranging this equation allows us to solve for the specific heat capacity of the metal:

Cmetal=−(mwater⋅Cwater⋅ΔTwater)mmetal⋅ΔTmetal​Let’s walk through a sample data set to experimentally determine the specific heat of an unknown metal –

Mass of metal 100.0 g
Initial Temperature of metal 100.0°C
Final temperature (metal & water) 25.0°C
Mass of water 150.0 g
Initial temperature of water 20.0°C
Specific Heat of Water 4.18 J/g·°C

Step 1 – Calculate the change in temperature

For the metal:

ΔTmetal=25.0∘C−100.0∘C=−75.0∘C\Delta T_{\text{metal}} = 25.0^\circ\text{C} – 100.0^\circ\text{C} = -75.0^\circ\text{C}

For the water:

ΔTwater=25.0∘C−20.0∘C=5.0∘C\Delta T_{\text{water}} = 25.0^\circ\text{C} – 20.0^\circ\text{C} = 5.0^\circ\text{C}

Step 2 – Use the specific heat equation

Cmetal=−(150.0g×4.18J/g∘C×5.0∘C)100.0g×(−75.0∘C)C_{\text{metal}} = \frac{- (150.0\ \text{g} \times 4.18\ \text{J/g}^\circ\text{C} \times 5.0^\circ\text{C})}{100.0\ \text{g} \times (-75.0^\circ\text{C})}

 

Cmetal=0.418J/g∘CC_{\text{metal}} = 0.418\ \text{J/g}^\circ\text{C}

The calculated specific heat is 0.418 J/g·°C, which is very close to the accepted value for copper.

Once your experimental value is calculated, you can compare it to the accepted value using percent error:

Percent Error=∣Experimental−Accepted∣Accepted×100%\text{Percent Error} = \frac{\left| \text{Experimental} – \text{Accepted} \right|}{\text{Accepted}} \times 100\%

Example: If the accepted value for copper is 0.390 J/g·°C:

Percent Error=∣0.418−0.390∣0.390×100%≈7.2%

This tells you how close your measurement is to the real value. A smaller percent error means your identification is likely correct. Your success depends on accurate measurements and careful handling of data—so take your time and double-check as you go!

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

Introductory Chemistry Lab Manual by Carol Stallworth is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book